Final recursion step
This section focuses on the final step of the proof recursion, where the last but one intermediate STARK proof, referred to as recursivef, is verified as well as the very last conversion of a STARK proof to a circuit.
Setup S2C for recursivef¶
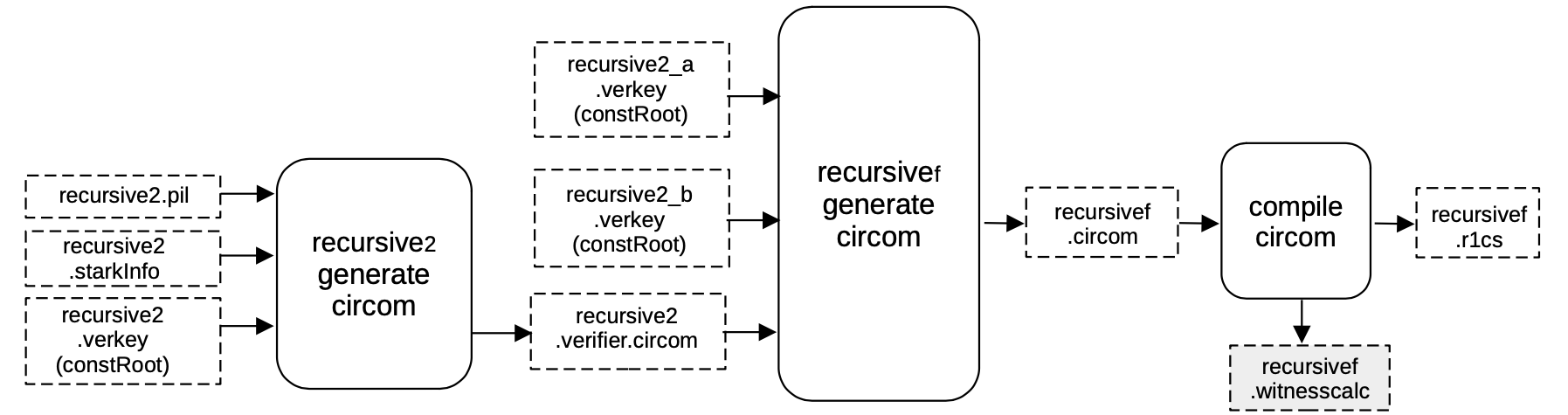
The idea here is the same as seen before when executing a S2C: It is to generate a CIRCOM circuit that verifies \(\mathtt{\pi_{rec2}}\), by mimicking the FRI verification procedure.
In order to achieve this, a verifier circuit recursive2.verifier.circom is generated from the previously obtained files;
- The
recursive2.pilfile, - The
recursive2.starkinfofile and - The constant roots of the previous two proofs \(\mathtt{recursive2\_} \texttt{a.verkey.constRoot}\) and \(\mathtt{recursive2\_b.} \texttt{verkey.constRoot}\);
by filling the \(\mathtt{stark\_} \texttt{verifier.circom.ejs}\) template.
The output CIRCOM file recursivef.circom, obtained by running a different script called genrecursivef, is in turn compiled into an R1CS recursivef.r1cs file and a $\text{witness calculator program`recursivef.witnesscal.
Both these outputs are used later on, to build and fill the next execution trace.
Setup C2S for recursivef¶
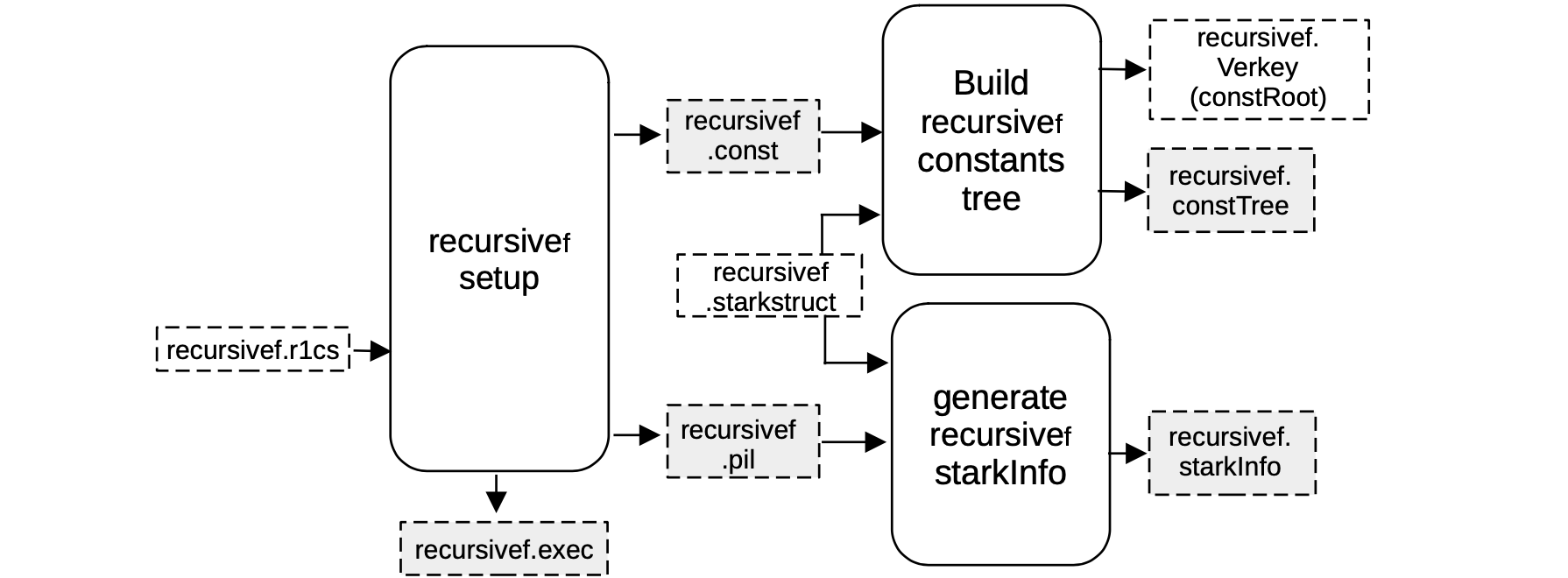
A C2S is again executed in this step. Hence a machine-like construction is obtained from the R1CS description of the verification circuit.
And, this construction must be the one whose execution correctness is equivalent to the validity of the previous circuit.
In this case, the R1CS description is in the file recursivef.r1cs, and the obtained construction is described by recursivef.pil.
Again, a binary for all the constant polynomials recursivef.const is generated, together with the helper file recursivef.exec, which provides allocation of the witness values into their corresponding positions in the execution trace.
Since all FRI-related parameters are stored in a recursive.starkstruct file, and this file is coupled with,
- the
recursivef.pilfile as inputs to the \(\mathtt{generate\_starkinfo}\) service in order to generate therecursivef.starkinfofile, and - the
recursivef.constas inputs to the component that builds the Merkle tree of evaluations of constant polynomials,recursivef.consttree, and its rootrecursivef.verkey.
Setup S2C for final¶
As done previously when executing a S2C, a CIRCOM circuit that verifies \(\mathtt{\pi_ {recf}}\) is generated by mimicking the FRI verification procedure.
In order to achieve this, a verifier circuit recursivef.verifier.circom is generated from the previously obtained files;
- The
recursivef.pilfile, - The
recursivef.starkinfofile and - The constant roots of the previous two proofs \(\mathtt{recursivef\_} \texttt{a.verkey.constRoot}\) and \(\mathtt{recursivef\_b.} \texttt{verkey.constRoot}\),
by filling the \(\mathtt{stark\_} \texttt{verifier.circom.ejs}\) template.
This verifier CIRCOM file gets imported by the final.circom circuit in order to generate the circuit being proved, using FFLONK procedure.
