Skip to content

Constructing simple SMTs

Understanding the finer details of how the Storage SM operates requires a good grasp of the way the zkProver’s Sparse Merkle Trees (SMTs) are constructed. This document explains how these SMTs are built.

Consider key-value pair based binary SMTs. The focus here is on explaining how to construct an SMT that represents a given set of key-value pairs. And, for the sake of simplicity, we assume 8-bit key-lengths.

A NULL or empty SMT has a zero root. That is, it has no key and no value recorded in it. Similarly, a zero node or NULL node refers to a node that carries no value.

A binary SMT with one key-value pair

A binary SMT with a single key-value pair \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\), is built as follows.

Suppose that \(K_{\mathbf{a}} = 11010110\). In order to build a binary SMT with this single key-value \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\),

  1. One computes the hash \(\mathbf{H}( \text{V}_{\mathbf{a}})\) of the value \(\text{V}_{\mathbf{a}}\),

  2. Sets the leaf \(\mathbf{L}_{\mathbf{a}} := \mathbf{H}( \text{V}_{\mathbf{a}})\),

  3. Sets the sibling leaf as a NULL leaf, simply represented as “\(\mathbf{0}\)”,

  4. Computes the root as \(\mathbf{root}_{a0} = \mathbf{H}(\mathbf{L}_{\mathbf{a}} \| \mathbf{0} )\), with the leaf \(\mathbf{L}_{\mathbf{a}}\) on the left because the \(\text{lsb}(K_{\mathbf{a}}) = 0\). That is, between the two edges leading up to the root, the leaf \(\mathbf{L}_{\mathbf{a}}\) is on the left edge, while the NULL leaf “\(\mathbf{0}\)” is on the right.

See the below figure for the SMT representing the single key-value pair \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\), where \(K_{\mathbf{a}} = 11010110\).

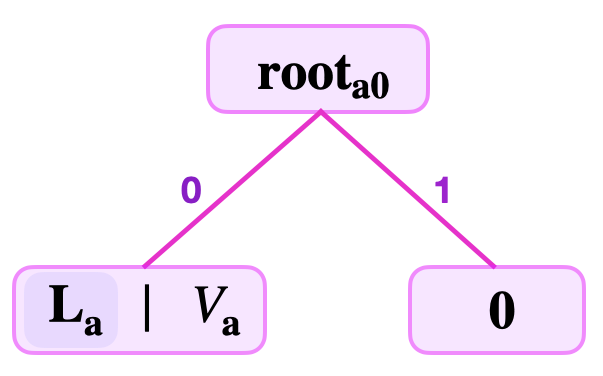
A Single key-value pair SMT

Note that the last nodes in binary SMT branches are generally either leaves or zero-nodes.

In the case where the least-significant bit, lsb of \(K_{\mathbf{a}}\) is \(1\), the SMT with a single key-value pair \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\) would be a mirror image of what is seen in Figure 3. And its root, \(\mathbf{root}_{0a} = \mathbf{H}( \mathbf{0}\| \mathbf{L}_{\mathbf{a}} ) \neq \mathbf{root}_{a0}\) because \(\mathbf{H}\) is a collision-resistant hash function.

This example also explains why we need a zero node. Since all trees used in our design are binary SMTs, a zero node is used as a default sibling for computing the parent node. This helps to differentiate between roots (also between parent nodes) because a root node actually identifies an SMT. Therefore, it is crucial to distinguish between \(\mathbf{root}_{a0} = \mathbf{H}(\mathbf{L}_{\mathbf{a}} \| \mathbf{0} )\) and \(\mathbf{root}_{0a} = \mathbf{H}( \mathbf{0}\| \mathbf{L}_{\mathbf{a}})\) because they represent two distinct trees.

Binary SMTs with two key-value pairs

Consider now SMTs with two key-value pairs, \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\) and \((K_{\mathbf{b}}, \text{V}_{\mathbf{b}})\).

There are three distinct cases of how corresponding SMTs can be built, each determined by the keys, \(K_{\mathbf{a}}\) and \(K_{\mathbf{b}}\).

Case 1

The keys are such that the \(\text{lsb}(K_{\mathbf{a}}) = 0\) and the \(\text{lsb}(K_{\mathbf{b}}) = 1\).

Suppose that the keys are given as \(K_{\mathbf{a}} = 11010110\) and \(K_{\mathbf{b}} = 11010101\).

To build a binary SMT with this two key-values, \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\) and \((K_{\mathbf{b}}, \text{V}_{\mathbf{b}})\),

  1. One computes the hashes, \(\mathbf{H}(\text{V}_{\mathbf{a}})\) and \(\mathbf{H}( \text{V}_{\mathbf{b}})\) of the values, \(\text{V}_{\mathbf{a}}\) and \(\text{V}_{\mathbf{b}}\) , respectively,

  2. Sets the leaves, \(\mathbf{L}_{\mathbf{a}} := \mathbf{H}( \text{V}_{\mathbf{a}})\) and \(\mathbf{L}_{\mathbf{b}} := \mathbf{H}( \text{V}_{\mathbf{b}})\),

  3. Checks if the \(\text{lsb}(K_{\mathbf{a}})\) differs from the \(\text{lsb}(K_{\mathbf{b}})\),

  4. Since the \(\text{lsb}(K_{\mathbf{a}}) = 0\) and the \(\text{lsb}(K_{\mathbf{b}}) = 1\), it means the two leaves can be siblings,

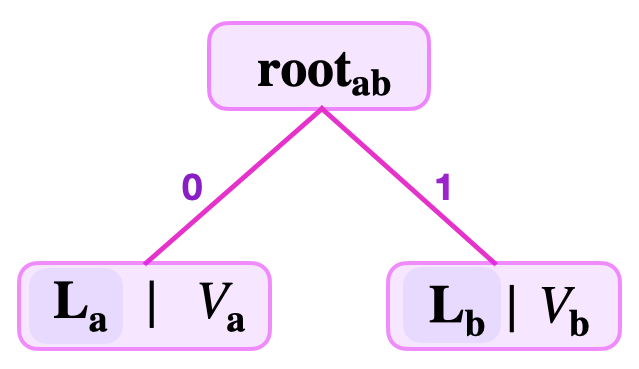
  5. One can then compute the root as, \(\mathbf{root}_{\mathbf{ab}} = \mathbf{H}(\mathbf{L}_{\mathbf{a}} \| \mathbf{L}_{\mathbf{b}})\).

Note that the leaf \(\mathbf{L}_{\mathbf{a}}\) is on the left because the \(\text{lsb}(K_{\mathbf{a}}) = 0\), but \(\mathbf{L}_{\mathbf{b}}\) is on the right because the \(\text{lsb}(K_{\mathbf{b}}) = 1\). That is, between the two edges leading up to the \(\mathbf{root}_{\mathbf{ab}}\), the leaf \(\mathbf{L}_{\mathbf{a}}\) must be on the edge from the left, while \(\mathbf{L}_{\mathbf{b}}\) is on the edge from the right.

See the below figure for the SMT representing the two key-value pairs \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\) and \((K_{\mathbf{b}}, \text{V}_{\mathbf{b}})\), where \(K_{\mathbf{a}} = 11010110\) and \(K_{\mathbf{b}} = 11010101\).

Two key-value pairs SMT - Case 1

Case 2

Both keys end with the same key-bit. That is, the \(\text{lsb}(K_{\mathbf{a}}) = \text{lsb}(K_{\mathbf{b}})\), but their second least-significant bits differ.

Suppose that the two keys are given as \(K_{\mathbf{a}} = 11010100\) and \(K_{\mathbf{b}} = 11010110\).

To build a binary SMT with this two key-values, \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\) and \((K_{\mathbf{b}}, \text{V}_{\mathbf{b}})\);

  1. One computes the hashes, \(\mathbf{H}(\text{V}_{\mathbf{a}})\) and \(\mathbf{H}( \text{V}_{\mathbf{b}})\) of the values, \(\text{V}_{\mathbf{a}}\) and \(\text{V}_{\mathbf{b}}\) , respectively.

  2. Sets the leaves, \(\mathbf{L}_{\mathbf{a}} := \mathbf{H}( \text{V}_{\mathbf{a}})\) and \(\mathbf{L}_{\mathbf{b}} := \mathbf{H}( \text{V}_{\mathbf{b}})\).

  3. Checks if the \(\text{lsb}(K_{\mathbf{a}})\) differs from the \(\text{lsb}(K_{\mathbf{b}})\). Since the \(\text{lsb}(K_{\mathbf{a}}) = 0\) and the \(\text{lsb}(K_{\mathbf{b}}) = 0\), it means the two leaves cannot be siblings at this position because it would otherwise mean they share the same tree-address 0, which is not allowed.

  4. One continues to check if the second least-significant bits of \(K_{\mathbf{a}}\) and \(K_{\mathbf{b}}\) differ. Since the \(\text{second lsb}(K_{\mathbf{a}}) = 0\) and the \(\text{second lsb}(K_{\mathbf{b}}) = 1\), it means the two leaves \(\mathbf{L}_{\mathbf{a}}\) and \(\mathbf{L}_{\mathbf{b}}\) can be siblings at their respective tree-addresses, 00 and 10.

  5. Next is to compute the hash \(\mathbf{H}(\mathbf{L}_{\mathbf{a}} \| \mathbf{L}_{\mathbf{b}})\) and set it as the branch \(\mathbf{B}_{\mathbf{ab}} := \mathbf{H}(\mathbf{L}_{\mathbf{a}} \| \mathbf{L}_{\mathbf{b}})\) at the tree-address 0. Note that the leaf \(\mathbf{L}_{\mathbf{a}}\) is on the left because the \(\text{second lsb}(K_{\mathbf{a}}) = 0\), while \(\mathbf{L}_{\mathbf{b}}\) is on the right because the \(\text{second lsb}(K_{\mathbf{b}}) = 1\).

  6. The branch \(\mathbf{B}_{\mathbf{ab}} := \mathbf{H}(\mathbf{L}_{\mathbf{a}} \| \mathbf{L}_{\mathbf{b}})\) needs a sibling. Since all the values, \(\text{V}_{\mathbf{a}}\) and \(\text{V}_{\mathbf{b}}\), are already represented in the tree at \(\mathbf{L}_{\mathbf{a}}\) and \(\mathbf{L}_{\mathbf{b}}\), respectively, one therefore sets a NULL leaf “\(\mathbf{0}\)” as the sibling leaf to \(\mathbf{B}_{\mathbf{ab}}\).

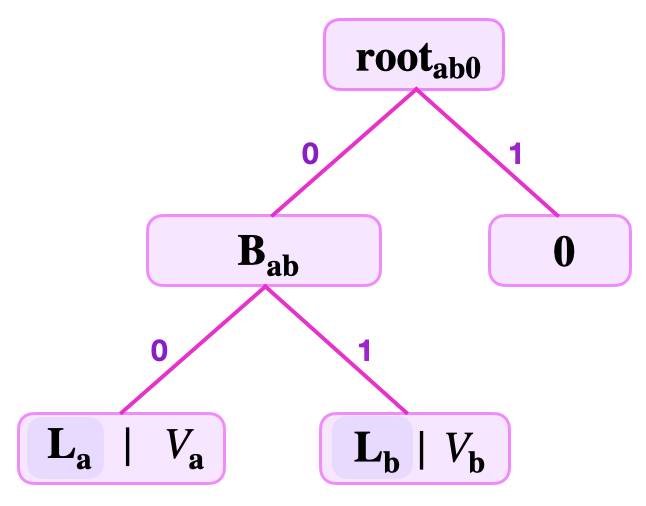
  7. As a result, it is possible to compute the root as, \(\mathbf{root}_{\mathbf{ab0}} = \mathbf{H}(\mathbf{B}_{\mathbf{ab}} \| \mathbf{0})\). Note that, the branch \(\mathbf{B}_{\mathbf{ab}}\) is on the left because the \(\text{lsb}(K_{\mathbf{a}}) = 0\), and \(\mathbf{0}\) must therefore be on the right. That is, between the two edges leading up to the \(\mathbf{root}_{\mathbf{ab0}}\), the branch \(\mathbf{B}_{\mathbf{ab}}\) must be on the edge from the left, while \(\mathbf{0}\) is on the edge from the right.

See the below figure depicting the SMT representing the two key-value pairs \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\) and \((K_{\mathbf{b}}, \text{V}_{\mathbf{b}})\), where \(K_{\mathbf{a}} = 11010100\) and \(K_{\mathbf{b}} = 11010110\).

Two key-value pairs SMT - Case 2

Case 3

The first two least-significant bits of both keys are the same, but their third least-significant bits differ.

Suppose that the two keys are given as \(K_{\mathbf{a}} = 11011000\) and \(K_{\mathbf{b}} = 10010100\). The process for building a binary SMT with these two key-values, \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\) and \((K_{\mathbf{b}}, \text{V}_{\mathbf{b}})\) is the same as in Case 2;

  1. One computes the hashes, \(\mathbf{H}(\text{V}_{\mathbf{a}})\) and \(\mathbf{H}( \text{V}_{\mathbf{b}})\) of the values, \(\text{V}_{\mathbf{a}}\) and \(\text{V}_{\mathbf{b}}\) , respectively.

  2. Sets the leaves, \(\mathbf{L}_{\mathbf{a}} := \mathbf{H}( \text{V}_{\mathbf{a}})\) and \(\mathbf{L}_{\mathbf{b}} := \mathbf{H}( \text{V}_{\mathbf{b}})\).

  3. Checks if the \(\text{lsb}(K_{\mathbf{a}})\) differs from the \(\text{lsb}(K_{\mathbf{b}})\). Since the \(\text{lsb}(K_{\mathbf{a}}) = 0\) and the \(\text{lsb}(K_{\mathbf{b}}) = 0\), it means the two leaves cannot be siblings at this position as it would otherwise mean they share the same tree-address 0, which is not allowed.

  4. Next verifier continues to check if the second least-significant bits of \(K_{\mathbf{a}}\) and \(K_{\mathbf{b}}\) differ. Since the \(\text{second lsb}(K_{\mathbf{a}}) = 0\) and the \(\text{second lsb}(K_{\mathbf{b}}) = 0\), it means the two leaves cannot be siblings at this position, because it would otherwise mean they share the same tree-address 00, which is not allowed.

  5. Once again he checks if the third least-significant bits of \(K_{\mathbf{a}}\) and \(K_{\mathbf{b}}\) differ. Since the \(\text{third lsb}(K_{\mathbf{a}}) = 0\) and the \(\text{third lsb}(K_{\mathbf{b}}) = 1\), it means the two leaves \(\mathbf{L}_{\mathbf{a}}\) and \(\mathbf{L}_{\mathbf{b}}\) can be siblings at their respective tree-addresses, 000 and 100.

  6. One then computes the hash \(\mathbf{H}(\mathbf{L}_{\mathbf{a}} \| \mathbf{L}_{\mathbf{b}})\), and sets it as the branch \(\mathbf{B}_{\mathbf{ab}} := \mathbf{H}(\mathbf{L}_{\mathbf{a}} \| \mathbf{L}_{\mathbf{b}})\) at the tree-address 00. The leaf \(\mathbf{L}_{\mathbf{a}}\) is on the left because the third \(\text{lsb}(K_{\mathbf{a}}) = 0\), while \(\mathbf{L}_{\mathbf{b}}\) is on the right because the third \(\text{lsb}(K_{\mathbf{b}}) = 1\).

  7. The branch \(\mathbf{B}_{\mathbf{ab}} := \mathbf{H}(\mathbf{L}_{\mathbf{a}} \| \mathbf{L}_{\mathbf{b}})\) needs a sibling. Since all the values, \(\text{V}_{\mathbf{a}}\) and \(\text{V}_{\mathbf{b}}\) , are already represented in the tree at \(\mathbf{L}_{\mathbf{a}}\) and \(\mathbf{L}_{\mathbf{b}}\), respectively, one therefore sets a NULL leaf “\(\mathbf{0}\)” as the sibling leaf to \(\mathbf{B}_{\mathbf{ab}}\).

  8. One can now compute the hash \(\mathbf{H}(\mathbf{B}_{\mathbf{ab}} \| \mathbf{0})\), and set it as the branch \(\mathbf{B}_{\mathbf{ab0}} := \mathbf{H}(\mathbf{B}_{\mathbf{ab}} \| \mathbf{0})\) at the tree-address 0. The hash is computed with the branch \(\mathbf{B}_{\mathbf{ab}}\) on the left because the second lsb of both keys, \(K_{\mathbf{a}}\) and \(K_{\mathbf{b}}\), equals \(0\). Therefore the NULL leaf “\(\mathbf{0}\)” must be on the right as an argument to the hash.

  9. The branch \(\mathbf{B}_{\mathbf{ab0}} := \mathbf{H}(\mathbf{B}_{\mathbf{ab}} \| \mathbf{0})\) also needs a sibling. For the same reason given above, one sets a NULL leaf “\(\mathbf{0}\)” as the sibling leaf to \(\mathbf{B}_{\mathbf{ab0}}\).

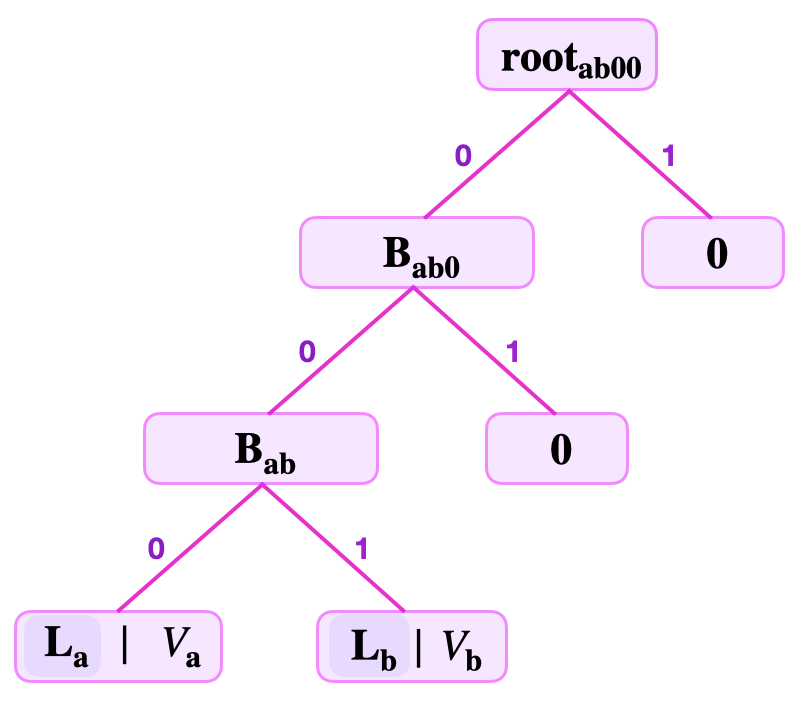
  10. Now, one is able to compute the root as \(\mathbf{root}_{\mathbf{ab00}} = \mathbf{H}(\mathbf{B}_{\mathbf{ab0}} \| \mathbf{0})\). Note that the hash is computed with the branch \(\mathbf{B}_{\mathbf{ab0}}\) on the left because the lsb of both keys, \(K_{\mathbf{a}}\) and \(K_{\mathbf{b}}\), equals \(0\). That is, between the two edges leading up to the \(\mathbf{root}_{\mathbf{ab00}}\), the branch \(\mathbf{B}_{\mathbf{ab0}}\) must be on the edge from the left, while “\(\mathbf{0}\)” is on the edge from the right.

See the below figure depicting the SMT representing the two key-value pairs \((K_{\mathbf{a}}, \text{V}_{\mathbf{a}})\) and \((K_{\mathbf{b}}, \text{V}_{\mathbf{b}})\), where \(K_{\mathbf{a}} = 11011000\) and \(K_{\mathbf{b}} = 10010100\).

Two key-value pairs SMT - Case 3

There are several other SMTs of two key-value pairs \((K_{\mathbf{x}}, \text{V}_{\mathbf{x}})\) and \((K_{\mathbf{z}}, \text{V}_{\mathbf{z}})\) that can be constructed depending on how long the strings of the common least-significant bits between \(K_{\mathbf{x}}\) and \(K_{\mathbf{z}}\) are.

In general, when building an SMT, leaves of key-value pairs with the same least-significant key-bits share the same navigational path only until any of the corresponding key-bits differ. These common strings of key-bits dictate where the leaf storing the corresponding value is located in the tree.

Last update: January 17, 2024
Authors: avenbreaks